Besucher:
 

zechow
rene

Zahlen, Ziffern und Nummern spielen eine wichtige Rolle in unserem Leben.
Auf ganz natürliche Weise gehen wir mit Ihnen von Kindesbeinen an um.

Auf dieser Seite stelle ich verschiedene Zahlensysteme vor und erkläre deren Gebrauch,
beziehungsweise (wenn möglich) deren Herkunft.

Unärsystem
Dualsystem
Ternärsystem
Dezimalsystem
Duodezimalsystem
Hexadezimalsystem
 

Zehow
Zechow
rené zechow

Unärsystem

Besser bekannt als Strichliste, ist das Unärsystem das einfachste Additionssystem bei dem jede
Stelle die Wertigkeit 1 besitzt.

Beispiel1:

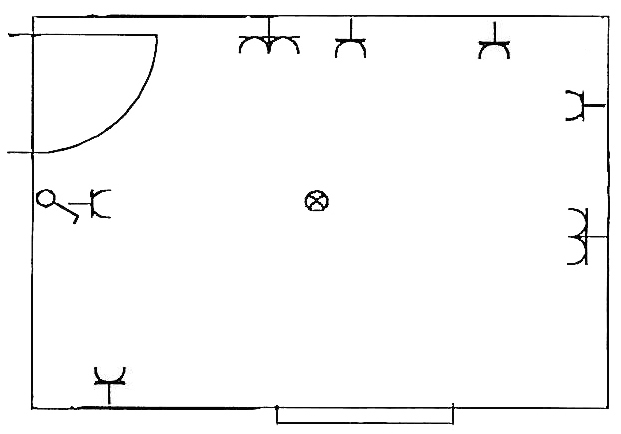
In einem Raum sollen Schalter, Steckdosen
und Abdeckrahmen gezählt werden.

Steckdosen:
IIII IIII  = 9

Ausschalter:
I = 1

Wippen für Ausschalter
I = 1

1-fach Rahmen:
IIII = 4

2fach Rahmen:
III = 3


Man beginnt mit dem Zählen von einem festen Punkt aus (zum Beispiel von der Tür)
und zählt dann immer in dieselbe Richtung (zum Beispiel im Uhrzeigersinn).
Üblicherweise wird jeder 5. Strich quer durch die vorherigen 4 geschrieben, um im nachhinein das
zusammenzählen zu vereinfachen.
Tipp: Um im oben genannten Beispiel die Anzahl der Schalter, Steckdosen und Rahmen zu überprüfen,
können die Zahlen gegengerechnet werden:
Rahmen: 4 x 1  + 3 x 2 = 10
Schalter,etc: 9 x 1  + 1 x 1 = 10
Stimmen die Zahlen überein, sollte man sich nicht verzählt haben!


Beispiel 2:
Auf einer Veranstaltung soll jeder Besucher gezählt werden (wir nehmen 24 Besucher an).

ohne Querstrich:
IIIIIIIIIIIIIIIIIIIIIIII

mit Querstrich:
IIII IIII   IIII IIII   IIII

Das Auszählen ohne Querstrich fällt uns relativ schwer, da es ab einer bestimmten Zahl sehr
unübersichtlich wird, und wir uns verzählen.
Da wir gewohnt sind im Dezimalsystem zu rechnen ist es einfacher die mit Querstrichen versehenen
Teilstriche zu addieren und mal fünf zu nehmen.
Im Beispiel 4 x 5 = 20,
und dann die restlichen Striche einfach zu addieren.
Im Bespiel 20 + 4 = 24. 
Um das Ganze noch einfacher zu gestalten, fügt man nach 10 Strichen einen Platzhalter, ein Komma
oder einen größeren Abstand zur nächsten Dekade ein.
Im Beispiel (2 x 10) + 4 = 24


Zurück nach oben (top)

Dualsystem (Binärsystem)

Das Dualsystem ist ein Stellenwertsystem mit der Basis 2.
Es ist neben dem Dezimalsystem wohl das wichtigste Zahlensystem, da es in der Digitaltechnik
fast unmöglich ist ein anderes System zu verwenden.
Es besticht durch seine Einfachheit - (Strom an = 1 / Strom aus = 0).
Der Name Dual (dualis - lat.: zwei enthaltend) trifft schon die Aussage, das nur 2 Ziffern in
diesem System enthalten sind, nämlich 0 und 1, die Bit (Binary digit) genannt werden.


Darstellung:
Jede Stelle besitzt eine gewisse Wertigkeit zur Basis 2. Beim Schreiben einer Dualzahl, sollte
stets ein Zusatz wie binär, (bin), b, B oder ₂ hinzugefügt werden,
um den Unterschied zum Dezimalsystem eindeutig festzulegen.
Beispiele zur Darstellung (dezimal 42):
- 101010_bin
- 101010₂
- 101010B


Ziffernfolge:
Zuerst sollte man die Ziffernfolge im Dualsystem kennen.
Hier der Vergleich Dezimal zu Dual.

Dezimal	Dual
0	0000 2
1	0001 2
2	0010 2
3	0011 2
4	0100 2
5	0101 2
6	0110 2
7	0111 2
8	1000 2
9	1001 2
10	1010 2
11	1011 2
12	1100 2
13	1101 2
14	1110 2
16	1111 2

Umrechnung dezimal nach dual:
Nehmen Sie die Dezimalzahl und teilen sie durch zwei.
Bleibt kein Rest ( xx,0 ) so notieren Sie eine 0.
Bleibt ein Rest ( xx,5 ) so notieren Sie eine 1.
Bei der Notierung schreiben Sie von rechts nach links.
Beispiel dezimal 42:

42 : 2 = 21 Rest 0 21 : 2 = 10 Rest 0,5 10 : 2 = 5 Rest 0 5 : 2 = 2 Rest 0,5 2 : 2 = 1 Rest 0 1 : 2 = 0 Rest 0,5 0 1 0 1 0 1

Ergebnis: 101010 _(bin)


Umrechnung dual nach dezimal:
Jede Stelle der Dualzahl hat den Wert einer Entsprechenden 2er Potenz.
Es wird also jede Stelle für sich ausgerechnet und die Teilergebnisse dann addiert.
Beginnen Sie auch hier auf der rechten Seite der Dualzahl.
Beispiel 101010 (bin)

0 1 0 1 0 1 x 2 0 x 2 1 x 2 2 x 2 3 x 2 4 x 2 5 (1) (2 x 1 = 2) (2 x 2 = 4) (2 x 2 x 2 = 8) (2 x 2 x 2 x 2 = 16) (2 x 2 x 2 x 2 x 2 = 32) 0 x 1 = 1 x 2 = 0 x 4 = 1 x 8 = 0 x 16 = 1 x 32 = 0 2 0 8 0 32 == 42

Aussprache, Binärpräfixe und Anderes
Wenn man in der Digitaltechnik von einem Bit (Binary digit) spricht, handelt es sich
um die zwei logischen Zustände 0 und 1. Es gibt noch weitere Begriffe, folgende
Tabellen sollen diese darstellen und erklären:

Name	in Bit	in Byte	in Wörtern
Bit	1 Bit
Nibble	4 Bit
Byte	8 Bit	1 Byte
Wort	16 Bit	2 Byte	1 Wort
Doppelwort	32 Bit	4 Byte	2 Wörter

Leider werden die Präfixe recht uneinheitlich verwendet. Nach dem internationalen
Einheitensystem (abgekürzt SI) basieren die Präfixe auf Zehnerpotenzen mit ganzzahligen Exponenten
Das Byte ist aber keine SI-Einheit. Daher gibt es eine Empfehlung, sogenannte Binärpräfixe
zu verwenden, die sich aber in der Praxis noch nicht durchgesetzt haben.
Hier eine Zusammenstellung
 
SI-Konform

Name	Bedeutung
kilobyte (kB)	103 Byte  = 1000 Byte
Megabyte (MB)	106 Byte  = 1.000.000 Byte
Gigabyte (GB)	109 Byte  = 1.000.000.000 Byte
Terrabyte (TB)	1012 Byte = 1.000.000.000.000 Byte
Petabyte (PB)	1015 Byte = 1.000.000.000.000.000 Byte

Binärpräfix

Name	Bedeutung
Kibibyte (KiB oder KB)	210 Byte = 1.024 Byte
Mebibyte (MiB)	220 Byte = 1.048.576 Byte
Gibibyte (GiB)	230 Byte = 1.073.741.824 Byte
Tebibyte (TiB)	240 Byte = 1.099.511.627.776 Byte
Pebibyte (PiB)	250 Byte = 1.125.899.906.842.624 Byte

Häufig wird zwar die SI-konforme Bedeutung ausgesprochen, jedoch die Binärpräfixe gemeint.
Doch schon bei einem kilobyte ist diese Abweichung 2,4%.
Beim Terrabyte entspricht die Abweichung zirka 10% !!
Hersteller von DVD Rohlingen geben die Kapazität Ihrer Produkte im SI-Einheitensystem an,
jedoch berechnen viele Softwaresysteme die Speichermedien mit Binärpräfixen,
was oft Verwirrung beim Anwender stiftet.
 

Zurück nach oben (top)

Ternärsystem

Das Ternärsystem ist ein Stellenwertsystem mit der Basis 3.
Analog zum Dualsystem wird eine Ziffer auch Trit genannt ( 0 , 1 , 2).


Umrechnung dezimal nach ternär:
Nehmen Sie die Dezimalzahl und teilen sie durch drei.
Bleibt kein Rest ( xx,0 ) so notieren Sie eine 0.
Bleibt ein Rest ( xx,3 ) so notieren Sie eine 1. (Merke 3:3 = 1 )
Bleibt ein Rest ( xx,6 ) so notieren Sie eine 2. (Merke 6:3 = 2 )
Bei der Notierung schreiben Sie von rechts nach links.
Beispiel dezimal 42:

42 : 3 = 14 Rest 0 14 : 3 = 4 Rest 0,6 4 : 3 = 1 Rest 0,3 1 : 3 = 0 Rest 0,3 0 2 1 1

Ergebnis 1120_(ter)


Umrechnung ternär nach dezimal:
Jede Stelle der Ternärzahl hat den Wert einer Entsprechenden 3er Potenz.
Es wird also jede Stelle für sich ausgerechnet und die Teilergebnisse dann addiert.
Beginnen Sie auch hier auf der rechten Seite der Ternärzahl.
Beispiel 1120 _(ter)

0 2 1 1 x 3 0 x 3 1 x 3 2 x 3 3 (1) (3 x 1 = 3) (3 x 3 = 9) (3 x 3 x 3 = 27) 0 x 1 = 2 x 3 = 1 x 9 = 1 x 27 = 0 6 9 27 == 42

Bedeutung in der Elektrotechnik:
Eigentlich ist das Ternärsystem unbedeutend, da in der Digitaltechnik eher das
Dualsystem verwendet wird.
Es wird aber unterschieden in gewöhnliches (wie oben beschrieben)
und balanciertes System. Beim balancierten Ternärsystem gibt es die
Ziffern 1 , 0 , -1.
Auf dieser Basis gab es in den 50er Jahren des letzten Jahrhunderts sogar
einen Computer (SETUN - nach einem Fluss der in der Nähe Moskauer Lomonossow-Universität)
in der Sowjetunion.

Wichtiger ist das ternäre Signal allerdings in der Übertragungstechnik,
wo es als Leitungscode eingesetzt wird. Die Bandbreite beträgt zirka 63% die für
binäre Übertragung nötig wäre. In der Praxis werden aber Codes verwendet die
diese Ersparnis zwar ausnutzen, jedoch für Redundanz, Taktrückgewinnung und
Fehlerkorrektur wieder verlieren.
Als pseudoternär gelten Leitungscodes, die zwar 3 Signalzustände haben, auf diesen
aber nur Binärsignale übertragen werden.
Hier einige Beispiele:


AMI-Code
(Alternate Mark Inversion)
Beim AMI-Code wird eine logische 0 mit der Spannung 0V übertragen.
Die logische 1 dagegen abwechselnd mit +U und -U. Dadurch wird ein Gleichstromanteil
vermieden. Der Nachteil, bei langen 0 Folgen, ist eine Taktrückgewinnung durch
den Empfäger nur schwer möglich.

HDB3-Code
(High Density Bipolar)
Der AMI-Code wird hierbei so abgeändert, das nach drei logischen 0 die nächste 0
in eine logische 1 verwandelt wird, die die gleiche Spannung, wie die letzte logische
1 hat. Dadurch wird eine Regelverletzung bewusst herbeigeführt. Da diese dem
Empfänger bekannt ist kann er diese Regelverletzung rückgängig machen.
Der Vorteil ist die Selbsttaktung des Signals, auch bei lägeren 0 Folgen.
Einsatzgebiet ist unter anderem auf PCM30 Übertragungsstrecken.


Modifizierter AMI-Code
Eine logische 1 wird mit der Spannung 0V übertragen.
Die logische 0 dagegen abwechselnd mit +U und -U.
Die Eigenschaften sind wie beim AMI-Code, allerdings kann sich bei
Mehrfachzugriff die logische 0 durchsetzen.
Einsatzgebiet ist zum Beispiel der D-Kanal im S0-Bus (D-Echokanal),
bei dem es durch Zugriff der TE (Terminal Equipment, maximal 8 dürfen
am S0-Bus angeschlossen sein) zu Kollisionen kommen kann.


4B3T-Code / MMS43
(4 Binär, 3 Tenär, auch als MMS43 - Modified Monitore Sum bekannt)
Vier Bits werden durch drei ternäre Symbole ersetzt.
Der Code ist gleichstromfrei, selbsttaktend, und belegt eine geringere
Bandbreite als pseudoternäre Codes. Der 4B3T-Code weist eine Effizienz
von 1,33 bit / Symbol auf.
Codetabelle des 4B3T-Codes

Binär	Spalte 1	Spalte 2	Spalte 3
0000	- - -		+ + +
0001	- - 0		+ + 0
0010	- 0 -		+ 0 +
0011	0 - -		0 + +
0100	- - +		+ + -
0101	- + -		+ - +
0110	+ - -		- + +
0111	- 0 0		+ 0 0
1000	0 - 0		0 + 0
1001	0 0 -		0 0 +
1010		0 + -
1011		0 - +
1100		+ - 0
1101		- 0 +
1110		+ - 0
1111		- + 0

von den 3³ = 27 Codewörtern wird 000 nicht benutzt.
Der 4B3T-Leitungscode wird für den Uk0 - Bus beim ISDN-Basisanschluß verwendet.



Zurück nach oben (top)

Dezimalsystem

Das Dezimalsystem ist ein Stellenwertsystem mit der Basis 10.
Es ist das am meisten verbreitete Zahlensystem überhaupt.
Die Wichtigste Erfindung hierbei war wohl die Ziffer 0.
Diese stellte den Durchbruch in der Mathematik dar, denn mit
Ihr konnte nun endlich im Stellenwertsystem gearbeitet werden.
Ein Übertrag auf die nächste Stelle beim erreichen der letzten
Ziffer war (und ist) eine Leichtigkeit. Heutzutage macht sich kaum
jemand Gedanken über diese Tatsache.
Aber die Basis 10 ist wohl für den Menschen das naheliegendste
Zahlensystem, besitzt er doch 10 Finger.
Über das 10er System muss ich wohl an dieser Stelle nichts mehr erzählen,
ausser Sie haben im Mathematikunterricht nicht richtig aufgepasst.
Wenn Sie dennoch weiterlesen habe ich ein paar Rechentricks für
Sie, mit denen Sie bei Kollegen oder Freunden Eindruck
schinden können.


Multiplizieren beliebiger Zahlen <20
Beispiel 1:
14 x 12
=> 14 + 2 = 160
=> 4 x 2 = 8
=> 160 + 8
=> Ergebnis 168.

Beispiel 2:
19 x 19
=> 19 + 9 = 280
=> 9 x 9 = 81
=> 280 +81
=> Ergebnis 361.

Beispiel 3:
15 x 17
=> 15 + 7 = 220
=> 5 x 7 = 35
=> 220 + 35
=> Ergebnis 255

Einfach oder?



Zurück nach oben (top)
 

Duodezimalsystem

Das Duodezimalsystem ist ein Stellenwertsystem mit der Basis 12.
Anders als das Dezimalsystem, besitzt das 12er System auch 12 Ziffern.
Dieses Zahlensystem ist weiter verbreitet als man glaubt. Ist doch die
Zahl Zwölf in vielen Sprachen ein eigenes Wort (eigentlich müsste es
zwei und zehn, bzw. zweizehn lauten).
Auch andere Begriffe wie “ein Dutzend” (12 Stück) haben noch heute
ihre Verwendung.
Im täglichen Leben fällt uns der Gebrauch des 12er Systems eigentlich
gar nicht mehr auf. Zum Beispiel hat das Jahr 12 Monate.
Unser Tag ist in 2 x 12 Stunden aufgeteilt.
Es gibt 12 Tierkreiszeichen am Nachthimmel zu Bewundern.
Die Zahl 12 hat relativ viele ganzzahlige Teiler: 1,2,3,4 und 6.
Vielleicht auch der Grund warum 12 Zoll ein Fuß sind.



Zurück nach oben (top)
 

Hexadezimalsystem

Das Hexadezimalsystem ist ein Stellenwertsystem mit der Basis 16.
Dieses System hat als Ziffern: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.
Der Name Hexadezimal setzt sich aus dem griechischen Wort Hexa (sechs)
und dem lateinischen Wort Decem (zehn) zusammen.
Hauptsächlich wird es in der Digitaltechnik verwendet, um Binäre Zustände
einfacher darzustellen. Sie können einfacher gelesen werden und
lassen sich wesentlich schneller schreiben.
4 Bit (1 Nibble) stellen eine Ziffer im Hexadezimalsystem dar.
Da es Zahlen über 10 beinhaltet, werden Ziffern über 9 mit Buchstaben
dargestellt.


Darstellung:
Jede Stelle besitzt eine gewisse Wertigkeit zur Basis 16. Beim Schreiben einer Hexadezimalzahl,
sollte stets ein Zusatz wie hex, (hex), $, H oder ₁₆ hinzugefügt werden,
um den Unterschied zum Dezimalsystem eindeutig festzulegen.
Beispiele zur Darstellung (dezimal 42):
- 2A_hex
- 2A₁₆
- $2A
- 0x2A


Ziffernfolge:
Zuerst sollte man die Ziffernfolge kennen. Hier der Vergleich von
Dezimaler zu Hexadezimaler und Binärer Darstellung.

Dezimal	Hexadezimal	Dual
0	$0	0000 2
1	$1	0001 2
2	$2	0010 2
3	$3	0011 2
4	$4	0100 2
5	$5	0101 2
6	$6	0110 2
7	$7	0111 2
8	$8	1000 2
9	$9	1001 2
10	$A	1010 2
11	$B	1011 2
12	$C	1100 2
13	$D	1101 2
14	$E	1110 2
15	$F	1111 2

Umrechnung dezimal nach hexadezimal:
Nehmen Sie die Dezimalzahl und teilen Sie diese durch 16.
Den Rest (Zahl,xxx) multiplizieren Sie wieder mit 16 und notieren die Ziffer.
Achtung! Bei Ergebnissen >9 werden Buchstaben als Ziffern verwendet.
Bei der Notierung schreiben Sie von rechts nach links.
Beispiel dezimal 8442:

8442 : 16 = 527 : 16 = 32 : 16 = 2 : 16 = 527,625 32,9375 2 0,125 Rest = 0,625 Rest = 0,9375 Rest = 0 Rest = 0,125 0,625 x 16 = 10 0,9374 x 16 = 15 0 x 16 = 0 0,125 x 16 = 2 A F 0 2

Ergebnis 20FA_(hex)


Umrechnung hexadezimal nach dezimal:
Jede Stelle der Hexadezimalzahl hat den Wert einer Entsprechenden 16er Potenz.
Es wird also jede Stelle für sich ausgerechnet und die Teilergebnisse dann addiert.
Beginnen Sie auch hier auf der rechten Seite der Hexadezimalzahl.
Beispiel 20FA _(hex)

A F 0 2 x 16 0 x 16 1 x 16 2 x 16 3 (1) (16 x 1 = 16) (16 x 16 = 256) (16 x 16 x 16 = 4096) 10 x 1 = 15 x 16 = 0 x 256 = 2 x 4096 = 10 240 0 8192 ==== 8442

Umrechnung hexadezimal nach dual
Das Umrechnen der Zahlensysteme Hexadezimal ins Dualsystem gestaltet sich
eigentlich sehr einfach, da 4 Bit (1 Nibble) genau einer Ziffer im Hexadezimal-
system entspricht und man somit nicht mit Resten oder Potenzen rechnen
muss. Anhand der oben aufgeführten Tabelle kann man die Zahlenwerte
einfach einsetzen.
Beispiel A42A_(hex)

$A $4 $2 $A = = = = 1010(2) 0100(2) 0010(2) 1010(2)

Ergebnis: 1010 0100 0010 1010_(bin)



Zurück nach oben (top)

Wenn Sie schon bis hier unten durchgedrungen sind und Sie die Seite aufmerksam
gelesen haben, werden Sie vielleicht festgestellt haben, das alle Rechenbeispiele
mit der Zahl 42 dargestellt wurden ( oder 42 rückwärts : 24 ).
Vielleicht sollten Sie mal Google fragen?

Mit freundlichem Gruß

René Zechow

 

Zechow,KNX , EIB , Website von René Zechow. Elektrotechniker Meister Elektrotechnik, Elektro, Strom, Funk, Wlan, Handy, Spannung Zeit, Autos, Gesellschaft, Würzburg, Würzburger, Altstadt, Frauenland, Heuchelhof, Sanderau, Würzburg.Zechow mit Informationen Würrzburg, 97,970,97074,97070,97072,97080,Höchberg,Zellerau, Reichenberg, Kist, Gerbrunn,Bayern, KNX, ABC, Schule, elektroinstallation, elektriker zechow, informationen, download, software von zechow, KNX, EIB,Zechow, suche,www.zechow.de, Elektro,elektrik, ellektriker,Technik, Telefon,telephone, telefonanlagen, tkanlage, itwissen,Zechow,rene,zechow, wichtige Informationen zur elektrotechnik von und mit rene zechow, alle rechte vorbehalten, google, suchmaschine,fireball,excite,altavista,windows,zechow,rheinsbergs,hotel,reise,alles was für die robots nötig ist, um meine seite zufinden. das sagt rene zechow, vielleicht hilfts was.zechow.zech,zecho,rene, strom , stromer

Zechow.de, von Rene Zechow, Würzburg, Elektrotechnik